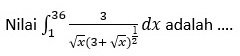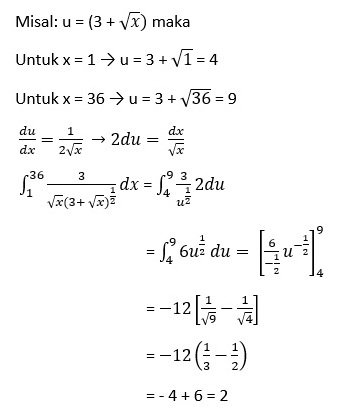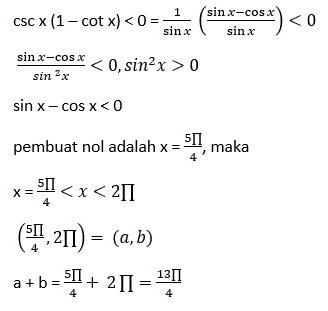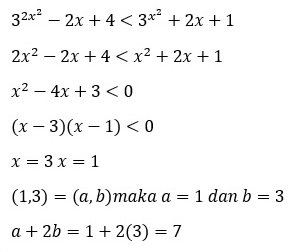15 Pembahasan Soal SBMPTN 2018 SAINTEK Matematika Kode Soal 434 No. 1 – 15

Soal SBMPTN 2018 SAINTEK No. 8

Jika panjang jari-jari lingkaran x² + y² + Ax + By – 4 = 0 adalah dua kali panjang jari-jari lingkaran yang x² + y² + Ax + By + 17 = 0, maka panjang jari-jari lingkaran yang lebih besar adalah …

A. √7

B. 2√7

C. 3√7

D. 4√7

E. 5√7

Jawaban: B

Pembahasan:

Soal SBMPTN 2018 SAINTEK No. 9

Sisa pembagian p(x) = x3 + ax2 + 3bx + 21 oleh x2 + 9 adalah b. Jika p(x) dibagi x + 1 bersisa 4b + 1, maka a + b = ….

A. 1

B. 2

C. 3

D. 4

E. 5

Jawaban: E

Pembahasan:

P(x) = x3 + ax2 + 3bx + 21 = (x2 + 9) (x + n) + b

P(x) = x3 + ax2 + 3bx + 21 = x3 + nx2 + 9x + 9n + b

• a = n
• 3b = 9 → b = 3

9n + b = 21

9n + 3 = 21

9n = 21 – 3

n = 18/9 = 2

a = n = 2

Jadi, a + b = 2 + 3 = 5

Soal SBMPTN 2018 SAINTEK No. 10

Jika garis singgu kurva y = 9 – x2 di titik P(a, b) dengan b>0 memotong sumbu x di titik Q(-5, 0), maka ab adalah …

A. -10

B. -8

C. 0

D. 8

E. 10

Jawaban: B

Pembahasan:

P(a, b) pada y = 9 – x2

b = 9 – a²

m = y^’ → m = -2x di titik (a, b)

m = -2a

y – b = -2a (x – a)

y – (9 – a²) = -2a (x – a)

melalui Q(-5, 0) maka,

-9 + a² = -2a (-5 -a)

-9 + a² = 10a + 2a²

0 = a² + 10a + 9

0 = (a + 1) (a + 9)

a = -1 dan a = -9

b = 8 dan b = -55

Jadi, a . b = -1 . 8 = -8

Soal SBMPTN 2018 SAINTEK No. 11

A. 1

B. 2

C. 3

D. 4

E. 5

Jawaban: B

Pembahasan:

Soal SBMPTN 2018 SAINTEK No. 12

Diketahui (an) dan (bn) adalah dua barisan aritmatika dengan a₁ = 5, a₂ = 8, b₁ = 3, dan b₂ = 7. Jika A = {a₁, a₂, … , a₁₀₀} dan B = {b₁, b₂, … , b₁₀₀}. Maka banyaknya anggota A Ç B adalah …

A. 20

B. 21

C. 22

D. 23

E. 24

Jawaban: 25

Pembahasan:

Aritmatika:

a₁ = 5

a₂ = 8

b₁ = 3

b₂ = 7

A = {a₁, a₂, …, a₁₀₀} → Un = 3n + 2

B = {b₁, b₂, …, b₁₀₀} → Un = 4n – 1

A = {5, 8, 11, 14, …, 302}

B = {3, 7, 11, 15, …, 399}

A Ç B = {11, 23, 35, …} → Un = 12n – 1

12n – 1 < 302

n < 25, 25

Jadi, n = 25

Soal SBMPTN 2018 SAINTEK No. 13

Himpunan semua bilangan real x pada selang (∏, 2∏) yang memenuhi csc x (1 – cot x) < 0 berbentuk (a, b). Nilai a + b adalah …

A. 9∏/4

B. 11∏/4

C. 3∏

D. 13∏/4

E. 15∏/4

Jawaban: D

Pembahasan:

Soal SBMPTN 2018 SAINTEK No. 14

Diketahui:

Jika (a, b) adalah interval dengan grafik y = f(x) berada di bawah grafik y = g(x), maka nilai a + 2b adalah …

A. 2

B. 4

C. 5

D. 7

E. 9

Jawaban: D

Pembahasan:

Soal SBMPTN 2018 SAINTEK No. 15

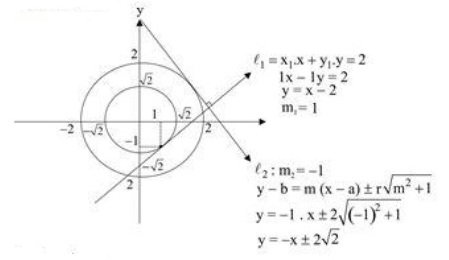
Diketahui dua lingkaran x² + y² = 2 dan x² + y² = 4. Garis I₁ menyinggung lingkaran pertama di titik (1, -1). Garis I₂ menyinggung lingkaran kedua dan tegak lurus dengan garis I₁. Titik potong garis I₁ dan I₂ adalah …

A. (1 + √2, √2 – 1)

B. (1 – √2, √2 – 1)

C. (1 + √2, √2 + 1)

D. (1 – √2, √2 – 2)

E. (1 + √2, √2 + 2)

Jawaban: A

Pembahasan:

 

Titik potong

y₁ = y₂

x – 2 = – x ± 2√2

2x = 2 ± 2√2

x = 1 ± 2√2

x₁ = 1 + √2

y₁ = 1 + √2 – 2

y₁ = -1 + √2

Titik (1 + √2, √2 -1)