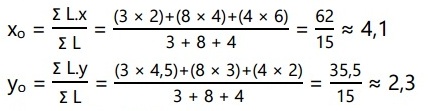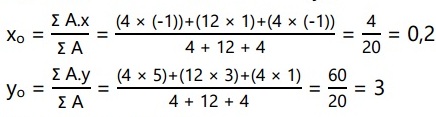Yuk kita pelajari soal dan pembahasan kesetimbangan benda tegar dan dinamika rotasi berikut ini.
Soal No. 1
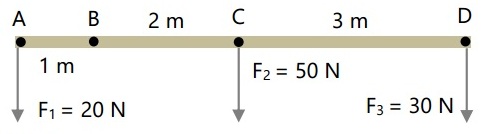
Tentukan torsi di titik A, B, C dan D pada batang homogen AD berikut!
Pembahasan:
Diketahui:
F1 = 20 N
F2 = 50 N
F3 = 30 N
dAB = 1 m
dAC = 3 m
dAD = 6 m
dBC = 2 m
dBD = 5 m
dCD = 3 m
Ditanyakan: ꚌA, ꚌB, ꚌC, ꚌD = ….?
Jawaban:
ꚌA = – (F2 . dAC) – (F3 . dAD)
ꚌA = – (50 N. 3 m) – (30 N . 6 m)
ꚌA = – 150 N.m – 180 N.m = – 330 N.m
ꚌB = (F1 . dAB) – (F2 . dBC) – (F3 . dBD)
ꚌB = (20N . 1m) – (50N . 2m) – (30N . 5m)
ꚌB = 20 N.m – 100 N.m – 150 N.m = – 220 N.m
ꚌC = (F1 . dAC) – (F3 . dCD)
ꚌC = (20 N . 3m) – (30 N . 3 m)
ꚌC =60 N.m – 90 N.m = – 30 N.m
ꚌD = (F1 . dAD) + (F2 . dCD)
ꚌD = (20N . 6m) + (50N . 3m)
ꚌD = 120 N.m + 150 N.m = 270 N.m
Soal No. 2
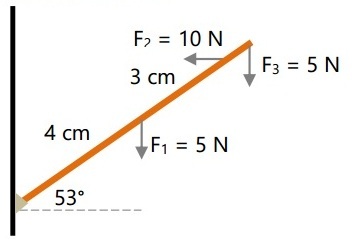
Tentukan torsi batang homogen berikut yang memiliki panjang 8 cm!
Pembahasan:
Diketahui:
F1 = 5 N
F2 = 10 N
F3 = 5 N
d1 = 4 cm = 0,04 m
d2 = 7 cm = 0,07 m
d3 = 8 cm = 0,08 m
ϴ = 530
Ditanyakan: ∑Ꚍ = …?
Jawaban:
∑Ꚍ = – (F1 . d1 cos ϴ) + (F2 . d2 sin ϴ) – (F3 . d3 cos ϴ)
∑Ꚍ = – (5 . 0,04 cos 530) + (10 . 0,07 sin 530) – (5 . 0,08 cos 530)
∑Ꚍ = – (0,2 . 3/5) + (0,7 . 4/5) – (0,4 . 3/5)
∑Ꚍ = – 0,12 + 0,56 – 0,24 = 0,2 N.m
Soal No. 3
Bola pejal 2 kg dengan jari – jari 10 cm yang awalnya ditahan menggelinding pada bidang miring 3,5 m licin dengan kemiringan 370. Berapa kecepatan bola ketika sampai di bawah?
Pembahasan:
Diketahui:
m = 2kg
r = 10 cm = 0,1 m
s = 3,5 m
ϴ = 370
Ditanyakan:
v = …?
Jawaban:
EP = EK translasi + EK rotasi
m . g. s . sinϴ = ½ . m . v2 . ½ . I . ω2
2 . 10 . 3,5 . sin 370 = ½ . 2 . v2 + ½ . 2/5 . 2 . r2 . v2/r2
70 . 3/5 = v2 + 2/5 v2
42 = 5/5 v2 + 2/5 v2
42 = 7/5 v2
7v2 = 42 x 5
v2 = 210/7
v2 = 30
v = √30 = 5,47 m/s
Soal No. 4
Silinder pejal berjari – jari 10 cm menggelinding di atas bidang miring kasar berkemiringan 300 dengan gaya sebesar 10 N pada pusat silinder diketahui nilai μk adalah 0,2.
Tentukan:
- Percepatan sudut silinder
- Energi kinetik silinder pada t = 4 s!
Pembahasan:
Diketahui:
r = 10 cm = 0,1 m
ϴ = 300
F = 10 N
μk = 0,2
Ditanyakan:
- α = …?
- EK pada t = 4 s = …?
Jawaban:
1. ∑F = W sin ϴ – f
10 = m . g . sin 300 – m . g . μk
10 = m . 10 . 0,5 – m . 10 . 0,2
10 = 5m – 2m
m = 10/3 kg
2. ωt = ω0 + α . t
ωt = 0 + 20 . 2
ωt = 40 rad/s
EK = ½ m . (ω . r)2 + ½ . I . ω2
EK = ½ 10/3 . (40 . 0,1)2 + ½ . ½ . 10/3 . 0,12 . 402
EK = 5/3 . 16 + 10/12 . 16
EK = 26,67 + 13,33 = 39 J
Soal No. 5
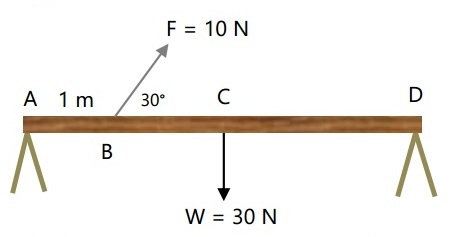
Perhatikan gambar berikut!
Sebuah batang AD homogen 4 m diletakkan di atas penyangga, A dan D dalam keadaan setimbang sesuai diagram di atas. Tentukan gaya ke atas yang dilakukan masing – masing penyangga, jika C merupakan titik berat benda!
Pembahasan:
Diketahui:
F = 10 N
W = 30N
ϴ = 300
d = 4 m
Ditanyakan: FA dan FD = …?
Jawaban:
ΣτD = 0
0 = -(FA. AD) +(F.BD sin30) -(W. CD)
0 = -(FA. 4) +(10. 3. 0,5) -(30. 2)
0 = -4.FA + 15 – 60
4FA = -45
FA = -11,25 N
ΣτA = 0
0 = (FD. AD) –(W. AC) -(F.AB sin30)
0 = (FD. 4) -(30. 2) -(10. 1. 0,5)
0 = 4.FD – 60 -5
4FD = 65
FD = 16,25 N
Jadi, gaya ke atas yang dilakukan masing – masing penyangga adalah -11,25 N dan 16,25 N.
Soal No. 6
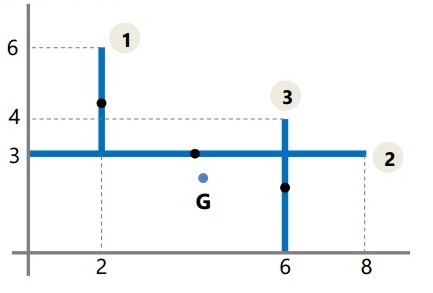
Tentukan titik berat sistem garis berikut pada bidang kartesius!
Pembahasan:
Diketahui:
| L1 = 3 | x1 = 2 | y1 = 4,5 |
| L1 = 8 | x1 = 4 | y1 = 3 |
| L1 = 4 | x1 = 6 | y1 = 2 |
Ditanyakan: Titik berat = …?
Jawaban:
Titik berat = (4,1; 2,3)
Soal No. 7
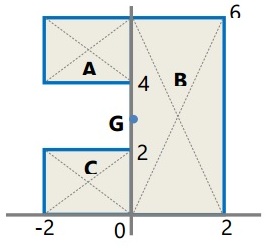
Tentukan titik berat bidang berikut!
Pembahasan:
Diketahui:
Diketahui:
| AA = 3 | xA = 2 | yA = 4,5 |
| AB = 8 | xB = 4 | yB = 3 |
| AC = 4 | xC = 6 | yC = 2 |
Ditanyakan: Titik berat = …?
Jawaban:
Titik berat = (4,1; 2,3)