Pengertian deret angka adalah penjumlahan suku-suku dari barisan tertentu. Perubahan di antara suku-suku berurutan dapat terjadi karena adanya pengurangan, penjumlahan, pembagian atau kelipatan bilangan tertentu. Untuk lebih memahaminya, perhatikan contoh soal cpns tentang deret angka berikut ini.
Soal No. 1
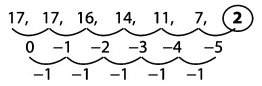
17, 17, 16, 14, 11, 7 ….
A. 0
B. 1
C. 2
D. 3
E. 4
Jawaban: C
Pembahasan:
Soal No. 2
2, 3, 5, 8, 13, 21, ….
A. 34
B. 35
C. 44
D. 45
E. 54
Jawaban: A
Pembahasan:
Pola bilangannya: 2, 3, 5, 8, 13, 21, …
Terlihat barisan Fibonacci di mana suatu suku merupakan jumlah dari dua suku sebelumnya.
5 = 2 + 3, 8 = 5 + 3, 13 = 8 +5, sehingga:
13 + 21 = 34
Soal No. 3
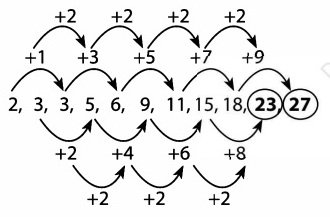
2, 3, 3, 5, 6, 9, 11, 15, 18, …, ….
A. 22, 28
B. 23, 29
C. 23, 27
D. 24, 26
E. 24, 29
Jawaban: C
Pembahasan:
Soal No. 4
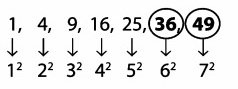
1, 4, 9, 16, 25, …, …
A. 36, 49
B. 36, 64
C. 49, 36
D. 49, 64
E. 64, 49
Jawaban: A
Pembahasan:
Soal No. 5
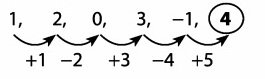
1, 2, 0, 3, -1, ….
A. -5
B. -4
C. 0
D. 4
E. 5
Jawaban: D
Pembahasan:
Soal No. 6
3, 7, 10, 17, 27, …, …, 115
A. 37, 44
B. 41, 74
C. 44, 64
D. 44, 71
E. 71, 115
Jawaban: D
Pembahasan:
Pola bilangannya: 3, 7, 10, 17, 27, …, …., 115
Terlihat barisan Fibonacci di mana suatu suku merupakan jumlah dari dua suku sebelumnya.
3 + 7 = 10
7 + 10 = 17
10 + 17 = 27
17 + 27 = 44
27 + 44 = 71
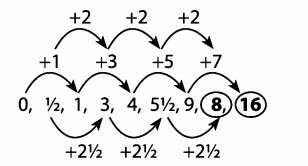
Soal No. 7
0, ½, 1, 3, 4, 5 ½, 9, …, …
A. 16, 18
B. 16, 19
C. 16, 8
D. 14, 8
E. 8, 16
Jawaban: E
Pembahasan:
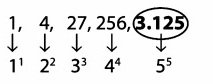
Soal No. 8
1, 4, 27, 256, …
A. 3.512
B. 3.325
C. 3.125
D. 2.315
E. 2.135
Jawaban: C
Pembahasan:
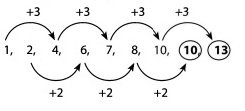
Soal No. 9
1, 2, 4, 6, 7, 8, 10, …, …
A. 15, 10
B. 15, 13
C. 13, 15
D. 13, 10
E. 10, 13
Jawaban: E
Pembahasan:
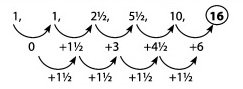
Soal No. 10
1, 2, 2 ½, 5 ½, 10, …
A. 17
B. 16
C. 15
D. 14
E. 13
Jawaban: B
Pembahasan: