Soal UN Fisika No. 16
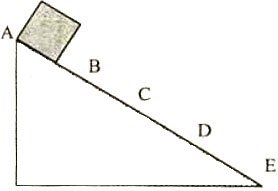
Sebuah balok dilepas tanpa kecepatan awal di puncak bidang miring licin (di A). balok meluncur hingga dasar bidang miring (di E).
Jika AB = BC = CD = DE maka perbandingan kecepatan balok di C, D, dan E adalah ….
A. 1 ∶ √2 ∶ √3
B. 1 ∶ √3 ∶ √2
C. √2 ∶ √3 ∶ 2
D. 2 ∶ √2 ∶ √3
E. 2 ∶ √3 ∶ √2
Pembahasan:
Diketahui:
Karena AB = BC = CD = DE, maka
hAB = 1
hAC = 2
hAD = 3
hAE = 4
Ditanyakan: vC : vD : vE …?
Jawaban:
vC : vD : vE = √(2ghAC) : √(2ghAD) : √(2ghAE)
vC : vD : vE = √hAC : √hAD : √hAE
vC : vD : vE = √2h : √3h : √4h
vC : vD : vE = √2 : √3 : 2
Jadi, perbandingan kecepatan balok di C, D, dan E adalah √2 : √3 : 2.
Soal UN Fisika No. 17
Anak panah dikaitkan pada tali busur, kemudian ditarik ke belakang dengan gaya 20 N sehingga tali busur meregang pada jarak 20 cm. Gesekan udara diabaikan, massa anak panah 250 gram maka kecepatan anak panah saat melesat dari busur adalah ….
A. 10 m.s−1
B. 5√3 m.s−1
C. 5 m.s−1
D. 4√2 m.s−1
E. 4 m.s−1
Pembahasan:
Diketahui:
F = 20 N
x = 20 cm = 0,2 m
m = 250 gr = 0,25 kg
Ditanyakan: v = …?
Jawaban:
EP = EK
½ F . x = ½ mv2
F . x = m . v2
v2 = F.x/m
v = √(F.x/m)
v = √(20 . 0,2 / 0,25)
v = √16 = 4 m.s-1
Jadi, kecepatan anak panah saat melesat dari busur adalah 4 m.s-1.
Soal UN Fisika No. 18
Seseorang yang bermassa 50 kg berdiri di atas perahu yang bermassa 200 kg. Perahu bergerak dengan kecepatan 7,5 m.s−1. Saat tiba di tempat tujuan, penumpang melompat dengan kecepatan 10 m.s−1 searah gerak perahu. Kelajuan perahu sesaat setelah penumpang melompat adalah ….
A. 0 m.s−1
B. 5,0 m.s−1
C. 6,9 m.s−1
D. 10,0 m.s−1
E. 11,9 m.s−1
Pembahasan:
Diketahui:
m1 = 50 kg
m2 = 200 kg
v = 7,5 m/s
v1’ = 10 m/s
Ditanyakan: v2’ = …?
Jawaban:
(m1 + m2) . v = m1 . v1’ + m2 . v2’
(50 kg + 200 kg) . 7,5 m/s = 50 kg . 10 m/s + 200 kg . v2’
1.875 kg.m/s = 50 kg.m/s + 200 kg . v2’
200 kg . v2’ = 1.875 kg.m/s – 50 kg.m/s
v2’ = 1.375 kg.m/s / 200 kg
v2’ = 6,9 m/s
Soal UN Fisika No. 19
Sebuah bola biliar A bermassa 100 gram bergerak menuju bola biliar B bermassa sama yang mula-mula dalam keadaan dam seperti gambar.
Besar kecepatan bola A sesudah tumbukan adalah ….
A. 5,0 m.s−1
B. √19 m.s−1
C. 4,0 m.s−1
D. √11 m.s−1
E. 3,0 m.s−1
Pembahasan:
Diketahui:
mA = mB = 100gr = 0,1 kg
v = 5 m.s-1
ϴ = 300
vBy‘ = 3 m.s-1
Ditanyakan: vA‘ = …?
Jawaban:
vAx = 5 cos 300 = 5/2 √3 m/s
vAy = 5 sin 300 = 5/2 m/s
vBx = vBy = 0 m/s
vBx‘ = 0 m/s
Tumbukan arah sumbu x:
mA . vAx + mB . vBx = mA . vAx‘ + mB . vBx‘
0,1 kg . 5/2 √3 m/s + 0,1 kg . 0 m/s = 0,1 kg . vAx‘ + 0,1 kg . 0 m/s
vAx‘ = 5/2 √3 m/s
Tumbukan arah sumbu y:
mA . vAy + mB . vBy = mA vAy‘ + mB . vBy‘
0,1 kg . 5/2 m/s + 0,1 kg . 0 m/s = 0,1 kg . vAy‘ + 0,1 kg . 3 m/s
5/2 m/s = vAy‘ + 3 m/s
vAy‘ = 5/2 m/s – 3 m/s = – ½ m/s
Setelah ketemu kecepatan tumbukan arah sumbu x dan sumbu y, sekarang kita bisa mencara kecepatan bola A setelah tumbukan.
vA‘ = √((vAx‘)2 + (vAy‘)2)
vA‘ = √((5/2 √3)2 + (- 1/2 )2)
vA‘ = √(75/4 + ¼)
vA‘ = √76/4 = √19
Jadi, kecepatan bola A setelah tumbukan sebesar √19 m.s-1.
Soal UN Fisika No. 20
Berikut data kalor jenis dari 4 zat padat:
| No. | Zat Padat | Kalor Jenis (J/kg0C) |
| 1 | Aluminium | 900 |
| 2 | Tungsten | 134 |
| 3 | Tembaga | 286 |
| 4 | Perak | 236 |
Keempat zat padat dengan massa yang sama diberi kalor juga dengan jumlah yang sama. Urutan zat yang mengalami kenaikan suhu dari tertinggi ke terendah adalah ….
A. aluminium – tembaga – perak – tungsten
B. tungsten – aluminium – tembaga – perak
C. tungsten – perak – tembaga – aluminium
D. perak – aluminium – tungsten – tembaga
E. perak – tembaga – tungsten – aluminium
Pembahasan:
Q = m . c . ∆t
∆t = Q/m . c
Karena kalor dan massa pada masing – masing zat adalah sama, maka perubahan suhu bergantung pada kalor jenis zat, semakin besar kalor jenis zat, maka perubahan suhunya semakin kecil dan sebaliknya, semakin kecil kalor jenis zat maka perubahan suhunya semakin besar.
Dengan demikian, urutan zat yang mengalami kenaikan suhu dari tertinggi ke terendah adalah tungsten – perak – tembaga – aluminium.