7 Contoh Soal Hukum Kekekalan Momentum Sudut pada Gerak Rotasi

Perhatikan contoh soal hukum kekekalan momentum sudut berikut ini.

Soal No. 1

Suatu partikel bermassa 2 kg berotasi dengan kelajuan sudut 4 rad/s. Jari – jari lintasan partikel tersebut adalah 1 m. Momentum sudut partikel tersebut adalah …

A. 2 kgm²rad/s

B. 3 kgm²rad/s

C. 5 kgm²rad/s

D. 8 kgm²rad/s

E. 10 kgm²rad/s

Jawaban: D

Pembahasan:

Diketahui:

m = 2 kg

ω = 2 rad/s

r = 1 m

Ditanyakan: L = …?

Jawaban:

L = I . ω

L = m . r² . ω

L = 2kg . 1 m² . 4 rad/s = 8 kgm²rad/s

Soal No. 2

Suatu benda mempunyai momen inersi 3 kgm² dan berotasi pada sumbu tetap dengan kecepatan sudur 2 rad/s. Momentum sudut benda tersebut adalah …

A. 2 kgm²rad/s

B. 4 kgm²rad/s

C. 6 kgm²rad/s

D. 8 kgm²rad/s

E. 10 kgm²rad/s

Jawaban: C

Pembahasan:

Diketahui:

I = 3 kgm²

ω = 2 rad/s

Ditanyakan: L = …?

Jawaban:

L = I . ω

L = 3 kgm² . 2 rad/s = 6 kgm²rad/s

Soal No. 3

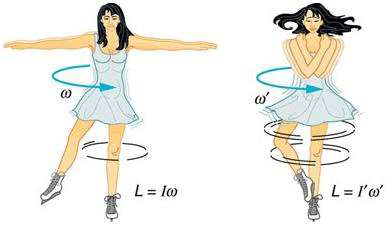
Seorang penari balet memiliki momen inersia 4kgm² ketika lengannya merapat ke tubuhnya dan 16 kgm² ketika lengannya terentang. Pada saat kedua lengannya dirapatkan ke tubuhnya, kelajuan putaran penari 12 putaran/s.

Jika kemudian kedua lengannya direntangkan, kelajuan putarannya menjadi …

A. 2 putaran/s

B. 3 putaran/s

C. 4 putaran/s

D. 5 putaran/s

E. 6 putaran/s

Jawaban: B

Pembahasan:

Diketahui:

I₁ = 4 kgm²

ω₁ = 12 putaran/s

I₂ = 16 kgm²

Ditanyakan: ω₂ = …?

Jawaban:

I₁ ω₁ = I₂ ω₂

4 kgm² . 12 putaran/s = 16 kgm² . ω

ω = 48/16 = 3 putaran/s.

Soal No. 4

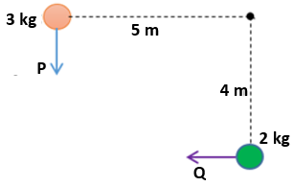
Perhatikan gambar berikut!

Gambar di atas menunjukkan posisi sesaat dari benda P dan Q yang sedang berotasi dengan kecepatan konstan masing – masing 1 m/s dan 3 m/s terhadap titik O dalam arah yang berlawanan. Momentum sudut total P dan Q terhadap O adalah …

A. 6 N.m

B. 9 N.m

C. 10 N.m

D. 12 N.m

E. 15 N.m

Jawaban: B

Pembahasan:

Diketahui:

m_P = 4 kg

v_P = 1 m/s

r_P = 5 m

m_Q = 2 kg

v_Q = 3 m/s

r_q = 4 m

Ditanyakan: L_O = …?

Jawaban:

L_O = L_P + L_Q

L_O = – (m_Pv_Pr_P) + (m_Qv_Qr_Q)

L_O = – (3 x 1 x 5) + ( 2 x 3 x 4)

L_O = -15 + 24 = 9 N.m

Soal No. 5

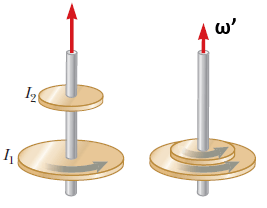
Perhatikan gambar berikut!

Roda 1 pada gambar yang memiliki massa 3 kg dan jari – jari 0,4 m berotasi dengan kecepatan sudut 50 rad/s. Roda 1 dikopel dengan roda 2 yang diam dan massa roda 2 kg dan jari – jarinya 0,2 m. Tentukan kecepatan sudut akhir bersama ω^’ setelah keduanya didorong hingga bersentuhan!

Pembahasan:

Diketahui:

m₁ = 3 kg

r₁ = 0,4 m

m₂ = 2 kg

r₂ = 0,2 m

ω₁ = 50 rad/s

ω₂ = 0 rad/s

Ditanyakan: ω^’ = …?

Jawaban:

L₁ = ½ m₁ . r₁² . ω₁

L₁ = ½ 3 . 0,4² .50 = 12 N.m

L₂ = ½ m₂ . r₂² . ω₂

L₂ = ½ 2 . 0,2² . 0 = 0 N.m

L^’ = (I₁ + I₂) ω^’

L^’ = (½ m₁ . r₁² + ½ m₂ . r₂²) ω^’

L^’ = (½ 3 . 0,4² + ½ 2 . 0,2²) ω^’

L^’ = 0,28 kg.m² . ω^’

L₁ + L₂ =L^’

12 N.m + 0 N.m = 0,28kgm² . ω^’

ω^’ = 12 N.m / 0,28 kgm² = 42,86 rad/s

Soal No. 6

Suatu benda mempunyai momen inersia 2kgm² dan berotasi pada sumbu tetap dengan kecepatan sudut 1 rad/s. Berapakah momentum sudut benda tersebut?

Pembahasan:

Diketahui:

I = 2 kgm²

ω = 1 rad/s

Ditanyakan: L = …?

Jawaban:

L = I . ω

L = 2 . 1 = 2 N.m

Soal No. 7

Perhatikan gambar berikut!

Bola pejal bermassa 2 kg dan berjari – jari 0,2 meter berotasi terhadap porosnya dengan kecepatan sudut 4 rad/s. Tentukan momentum sudut bola pejal tersebut!

Pembahasan:

Diketahui:

m = 2 kg

r = 0,2 m

ω = 4 rad/s

Ditanyakan: L = …?

Jawaban:

L = I . ω

L = 2/5 m r² ω

L = 2/5 . 2 . 0,2² . 4 = 0,128 N.m