Materi Torsi dan Momen Inersia

A. Torsi atau Momen Gaya

Pengertian torsi atau momen gaya adalah besaran vektor hasil perkalian silang antara vektor posisi r dengan gaya F. Yang secara matematis dituliskan sebagai berikut:

τ = F . r . sin ϴ

Keterangan:

τ = Torsi (N.m)

F = Gaya (N)

r = Jarak gaya ke poros/Vektor posisi (m)

ϴ = sudut gaya

1. Torsi bernilai positif, jika arahnya berlawanan jarum jam.
2. Torsi bernilai negatif, jika arahnya searah jarum jam.

Contoh Soal:

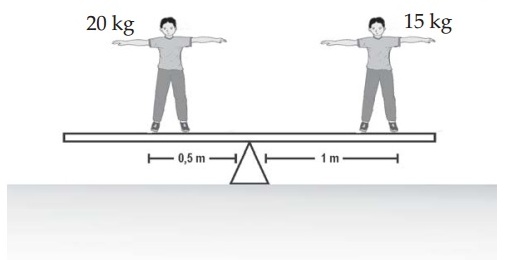
Perhatikan gambar berikut!

Salah satu ujung sebuah jungkat – jungkit dinaiki anak yang massanya 15 kg. Ujung satunya dinaiki anak yang massanya 20 kg. Jarak masing – masing anak dari titik tumpu adalah 1 m dan 0,5 m. Berapa torsi masing – masing dan berapa torsi totalnya? Kemana arah putaran batang? (g = 10  m/s²)

Pembahasan:

Diketahui:

m1 = 15 kg

m2 = 20 kg

r1 = 1 m

r2 = 0,5 m

g = 10  m/s²

ϴ1 = 90⁰

ϴ2 = 90⁰

Ditanyakan: τ = …?

Jawaban:

τ1 = F . r . sin ϴ

τ1 = (m.g) . r . sin 90⁰

τ1 = 15 kg . 10 m/s² . 1 m . 1 = 150 N.m

τ2 = F . r . sin ϴ

τ2 = (m.g) . r . sin 90⁰

τ2 = 20 kg . 10 m/s² . 0,5 m . 1 = 100 N.m

∑τ = τ1 – τ2 150 N.m – 100 N.m

Arah putaran searah jarum jam.

B. Momen Inersia

Momen inersia didefinisikan sebagai hasil kali massa partikel dengan kuadrat jarak yang tegak lurus dari titik poros rotasi. Besar momen inersia bergantung pada massa dan jarak dari sumbu rotis. Semakin jauh dari sumbu rotasi maka momen inersianya akan semakin besar. Yang secara matematis dituliskan sebagai berikut:

I = m . r²

Keterangan:

I = momen inersia (kg.m²)

m = massa (kg)

r = jarak (m²)

Jika suatu benda memiliki poros rotasi tidak di ujung benda tersebut, maka benda tersebut dianggap terdiri dari dua benda dengan nilai momen inersianya masing – masing.

Contoh Soal:

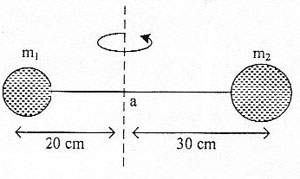
Dua bola masing – masing massanya m₁ = 2kg dan m₂ 3 kg dihubungkan dengan batang ringan tak bermassa seperti pada gambar.

Jika sistem bola diputar pada sumbu di titik a, besar momen inersia sistem bola adalah …

A. 0,24 kg.m²

B. 0,27 kg.m²

C. 0,30 kg.m²

D. 0,31 kg.m²

E. 0,35 kg.m²

Pembahasan:

Diketahui:

m₁ = 2 kg

m₂ = 3 kg

r₁ = 20 cm = 0,2 m

r₂ = 30 cm = 0,3 m

Ditanyakan: I =…?

Jawaban:

I = m₁r₁² + m₂r₂²

I = 2 x 0,2² + 3 x 0,3²

I = 0,08 kg.m² + 0,27 kg.m²

I = 0,35 kg.m²

C. Momen Inersia untuk Berbagai benda pada Berbagai Sumbu Rotasi​

No.	Benda	Gambar	Rumus
1	Kulit silinder terhadap sumbu yang lewat pusat silinder		I = m . r2
2	Kulit silinder yang panjangnya l terhadap diameter yang lewat pusat		I = ½ m . r2 + ½ m . l2
3	Silinder pejal terhadap sumbu		I = ½ m . r2
4	Silinder pejal berjari – jari r, panjangnya l terhadap diameter yang melalui pusat		I = ¼ m . r2 + 1/12 m . l2
5	Batang tipis terhadap garis tegak lurus melalui salah satu ujungnya		I = 1/3 m . l2
6	Kulit bola tipis berjari – jari r terhadap diameternya		I = 2/3 m . r2
7	Batang tipis terhadap garis tegak lurus yang melalui pusat		I = 1/12 m . r2
8	Balok padat terhadap sumbu yang melalui pusat tegak lurus pada permukaan		I = m/12 (a2 + b2)
9	Bola pejal berjari – jari r terhadap diameternya		I = 2/5 m . r2