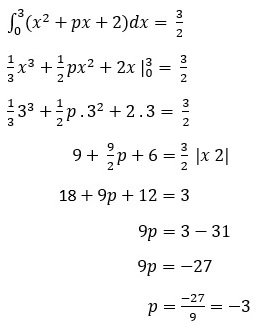40 Soal UN Matematika SMA 2018 dan Pembahasannya

Soal No. 21

Diketahui

Nilai p yang memenuhi adalah ….

A.   −26

B.   −13

C.   −3

D.   3

E.   13

Jawaban: C

Pembahasan:

Soal No. 22

Diketahui segitiga ABC siku-siku di B dan sin⁡ R = 8/17 (P dan R sudut lancip). Nilai dari (1 − cos ⁡R)(1 + sin ⁡P) adalah ….

A.   17/8

B.   17/15

C.   64/289

D.   −64/289

E.   −225/289

Jawaban: C

Pembahasan:

Diketahui:

sin⁡ R = 8/17, maka sistem trigonometri yang berlaku adalah

sisi depan = 8

sisi miring = 17

sisi samping = 15

Ditanyakan: Nilai dari (1 − cos ⁡R)(1 + sin ⁡P) = …?

Jawab:

cos ⁡R = 15/17 dan sin ⁡P = 15/17

(1 − cos ⁡R)(1 + sin ⁡P)

= (1 – 15/17)(1 + 15/17)

= (2/17) (32/17)

= 64/289

Soal No. 23

Sisno diminta mengukur tinggi tiang bendera menggunakan klinometer.

Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut 60°. Kemudian ia bergerak menjauhi tiang bendera sejauh 10 m dan terlihat pada klinometer sudut 45°. Tinggi tang bendera adalah ….

A.   (15 + 10√3) m

B.   (15 + 5√3) m

C.   (15 − 5√3) m

D.   (15 − 10√3) m

E.   (5 + 10√3) m

Jawaban: B

Pembahasan:

tan⁡ 60° = t/x

√3 = t/x

t = √3 x

tan⁡ 45° = t/(x + 10)

1 = t/(x + 10)

t = x + 10

√3 x = x + 10

√3 x − x = 10

(√3 − 1)x = 10

x = 10/(√3 − 1)

t = x + 10
= 5√3 + 5 + 10
= 15 + 5√3

Soal No. 24

Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60° dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter maka luas taman tersebut adalah ….

A.   72 m²

B.   72√2 m²

C.   72√3 m²

D.   144 m²

E.   144√3 m²

Jawaban: C

Pembahasan:

L = 1/2 ab sin ⁡α

L = 1/2 × 18 × 16 × sin 60°

L = 1/2 × 18 × 16 × 1/2 √3

L = 9 × 8√3  = 72√3

Soal No. 25