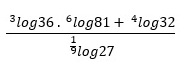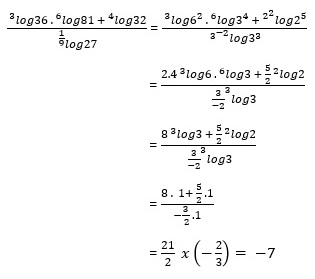Soal UN matematika SMA 2018 berikut ini telah dilengkapi dengan pembahasannya sehingga kamu bisa lebih mudah dalam mempelajarinya. Yuk langsung saja dipelajari.
Soal No. 1
Hasil dari
adalah …
A. 11
B. 7
C. 4
D. -7
E. -11
Jawaban: D
Pembahasan:
Soal No. 2
Diketahui f(x) = 3x + 2 dan (g ∘ f)(x) = 6x − 4. Nilai g−1 (−4) = ….
A. 4
B. 2
C. 1
D. −2
E. −4
Jawaban: B
Pembahasan:
Diketahui:
f(x) = 3x + 2
maka,
f−1(x) = ⅓(x − 2)
Jika,
(g ∘ f)(x) = ax + b
maka,
g(x) = af−1(x) + b
g(f(x)) = 6x − 4
g(x) = 6f−1(x) − 4
g(x) = 6[⅓(x − 2)] − 4
g(x) = 2x − 4 − 4
g(x) = 2x − 8
g−1(x) = 1/2(x + 8)
g−1(−4) = 1/2 (−4 + 8)
g−1(−4) = 1/2 × 4 = 2
Soal No. 3
Dina harus membantu orang tuanya berjualan bahan makanan di toko keluarganya. Dina mendapat uang saku berdasarkan jumlah barang yang terjual pada hari tersebut dengan fungsi U(x) = 1.500x + 500, dengan U adalah uang saku dalam rupiah dan x adalah jumlah barang dalam unit. Jika jumlah barang yang terjual tergantung pada waktu yang dihabiskan Dina di toko keluarganya dengan x(t) = 2t + 3, di mana t adalah waktu dalam jam, maka besar uang saku Dina jika dia membantu selama 2 jam pada suatu hari adalah ….
A. Rp 10.500,00
B. Rp 11.000,00
C. Rp 11.500,00
D. Rp 12.500,00
E. Rp 12.500,00
Jawaban: B
Pembahasan:
Diketahui:
U(x) = 1.500x + 500
x(t) = 2t + 3
t = 2 jam
Ditanyakan: U(x) = …?
Jawaban:
x(t) = 2t + 3
x(2) = 2 ∙ 2 + 3
x(2) = 4 + 3 = 7
U(x) = 1.500x + 500
U(7) = 1.500 ∙ 7 + 500
U(7)= 10.500 + 500 = 11.000
Soal No. 4
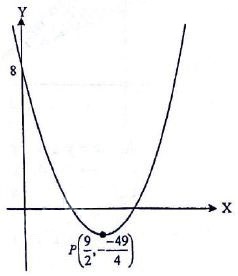
Diketahui grafik fungsi kuadrat seperti pada gambar.
Koordinat titik potong grafik dengan sumbu x adalah ….
A. (−1, 0) dan (−8, 0)
B. (−1, 0) dan (8, 0)
C. (1, 0) dan (−8, 0)
D. (1, 0) dan (8, 0)
E. (2, 0) dan (5, 0)
Jawaban: D
Pembahasan:
Fungsi kuadrat pada titik (9/2, −49/4) adalah:
y = a(x − 9/2)2 − 49/4
Seperti yang kita lihat dalam grafik bahwa fungsi kuadrat tersebut melalui titik (0, 8). Oleh sebab itu, kita bisa mencari nilai a dengan cara mensubstitusikan fungsi kuadrat tersebut dengan titik (0, 8).
y = a(x − 9/2)2 − 49/4
8 = a(0 − 9/2)2 − 49/4
8 = 81/4 a − 49/4 |x4|
32 = 81a − 49
81a = 32 + 49
81a = 81
a = 1
Sehingga, dengan memasukkan nilai a, fungsi kuadrat tersebut menjadi:
y = a(x − 9/2)2 − 49/4
y = 1(x − 9/2)2 − 49/4
y = x2 − 9x + 81/4 − 49/4
y = x2 − 9x + 8
Kini, kita bisa menentukan koordinat titik potong grafiknya dengan sumbu x:
y = 0
x2 − 9x + 8 = 0
(x − 1)(x − 8) = 0
x = 1 atau x = 8
Soal No. 5
Batas nilai m agar persamaan kuadrat (m + 3)x2 + mx + 1 = 0 mempunyai akar-akar riil adalah ….
A. 2 ≤ m ≤ 6
B. −2 ≤ m < 6
C. m ≤ −2 atau m ≥ 6
D. m ≤ −2 atau m > 6
E. m ≤ −6 atau m ≥ −2
Jawaban: C
Pembahasan:
akar riil dari (m + 3)x2 + mx + 1 = 0 adalah
b2 − 4ac ≥ 0
m2 − 4(m + 3)1 ≥ 0
m2 − 4m − 12 ≥ 0
(m + 2)(m − 6) ≥ 0
m ≤ −2 atau m ≥ 6