40 Soal UN Matematika SMA 2018 dan Pembahasannya

Soal No. 6

Pada tahun 2016, umur seorang ibu tiga kali umur anaknya. Pada tahun 2010 umur ibu lima kali umur anaknya. Jumlah umur mereka pada tahun 2020 adalah ….

A.   52 tahun

B.   54 tahun

C.   56 tahun

D.   62 tahun

E.   64 tahun

Jawaban: C

Pembahasan:

Kita anggap:

umur ibu = x

umur anak = y

Pada tahun 2016, umur ibu 3 kali umur anak, sehingga:

x = 3y

dan pada tahun 2010, namun karyang berarti umurnya berkurang 6 tahun dari tahun 2016, umur ibu 5 kali umur anak, sehingga:

x − 6 = 5(y − 6) 

x − 6 = 5y − 30
x = 5y − 24   

Untuk mengetahui berapa umur ibu dan anak pada tahun 2016, kita substitusikan kedua persamaan di atas:

x = 5y − 24   

3y = 5y − 24   

2y = 24

y = 12 tahun

Jadi, kita umur anak pada tahun 2016 adalah 12 tahun, sedangkan umur ibu yaitu:

x = 3y

x = 3 x 12 = 36 tahun

Jumlah umur mereka pada tahun 2020 (4 tahun dari tahun 2016), yaitu:

Umur ibu = 36 + 4 = 40 tahun

Umur anak = 12 + 4 = 16 tahun

Umur ibu + umur anak = 40 tahun + 16 tahun = 56 tahun.

Soal No. 7

Keliling sebuah persegi panjang 28 cm, sedangkan panjangnya 2 cm lebih panjang dari lebarnya. Luas dari persegi panjang adalah ….

A.   48 cm²

B.   44 cm²

C.   28 cm²

D.   14 cm²

E.   8 cm²

Jawaban: A

Pembahasan:

Diketahui:

K = 28 cm

p = (l + 2) cm 

Ditanyakan: L = …?

Jawaban:

L = p × l

Oleh sebab itu, kita perlu mencari nilai l nya terlebih dahulu.

K = 28

2(p + l) = 28

p + l = 14

l + 2 + l = 14

2l + 2 = 14

2l = 12

l = 6 cm

Setelah ketemu nilai l, kita bisa nyari nilai p nya, dengan cara:

p = (l + 2)

p = 6 + 2 = 8 cm

Sehingga, nilai luasnya adalah :

L = p × l

L = 8 cm x 6 cm = 48 cm²

Soal No. 8

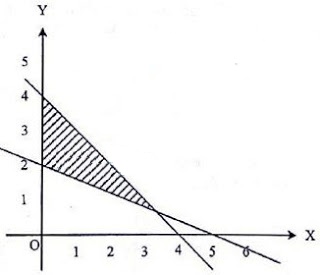
Daerah yang diarsir pada gambar di bawah ini adalah daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan ….

A.   x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0

B.   x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0

C.   x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0

D.   x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0

E.   x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0

Jawaban: C

Soal No. 9

Untuk membuat 1 liter minuman jenis A diperlukan 2 kaleng soda dan 1 kaleng susu, sedangkan untuk membuat 1 liter minuman jenis B diperlukan 2 kaleng soda dan 3 kaleng susu. Tersedia 40 kaleng soda dan 30 kaleng susu. Jika 1 liter minuman jenis A dijual seharga Rp 30.000,00 dan satu liter minuman jenis B dijual seharga Rp 50.000,00, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah ….

A.   Rp 500.000,00

B.   Rp 540.000,00

C.   Rp 600.000,00

D.   Rp 700.000,00

E.   Rp 720.000,00

Jawaban: D

Pembahasan:

Diketahui:

	Minuman Jenis A	Minuman Jenis B	Stok
Soda	2	2	40
Susu	1	3	30
Harga Jual	Rp 30.000	Rp 50.000	?

Ditanyakan: Pendapatan maksimum dari hasil penjualan kedua jenis minuman = …?

Jawaban:

Jumlah soda yaitu:

2A + 2B = 40 |:2|

Kita sederhanakan (dibagi 2) menjadi:

1A + 1B = 20

Kemudian kita eliminasikan antara soda dan susu:

1A + 1B = 20

1A + 3B = 30

—————- –

2B = 10

B = 5

Setelah ketemu nilai B, kemudian kita substitusikan untuk mencari nilai A

1A + 1B = 20

A + 1 x 5 = 20

A = 20 – 5 = 15

Jika 1 liter minuman jenis A dijual seharga Rp 30.000,00 dan satu liter minuman jenis B dijual seharga Rp 50.000,00, maka:

Pendapatan maksimum = (Rp 30.000 x 15) + (Rp 50.000 x 5) = Rp 700.000

Soal No. 10

Diketahui matriks

Jika matriks C = AB, invers matriks C adalah C⁻¹ = ….

Jawaban: B

Pembahasan: